SSI y MSI

SSI y MSI son niveles de integración de compuertas lógicas.

Los niveles de integración son:

SSI: (Small-Scale Integration o integración a pequeña escala). Es el nivel de integración más básico y comprende todos aquellos circuitos integrados (desde ahora IC por sus siglas en inglés) que poseen hasta un máximo de diez (10) compuertas. En este nivel tenemos las compuertas lógicas como las NAND (por ejemplo, el IC 7400 tiene 4 compuertas NAND de dos entradas), las NOT (IC 7404 con 6 compuertas NOT), las AND (IC 7408 de 4x2), las OR (IC 7432 de 4x2), las XOR (IC 7486), memorias de 1 bit, flip-flops, el IC7480 que es un sumador completo de 1 bit, etc. Estas compuertas integran de 10 a 100 transistores.

MSI: (Medium-Scale Integration o integración de mediana escala). Es el nivel de integración que le sigue al SSI. Comprenden IC de que tienen entre 10 y 100 compuertas (entre 100 y 1000 transistores). En este campo tenemos memorias de palabra (8 bits), multiplexores, decodificadores, sumadores completos -entre ellos el IC7482 que es de 2 bits y el 7483 que es de 4 bits-, registros, contadores, etc.)

DECODIFICADORES: un decidificador es un cicuito combinacional que convierte la informacion binaria de n lineas de entradas a un maximo de 2^n lineas unicas de salida. para cada una de las combinaciones de entrada solo una de las salidas estara activada con un 1 (para cuando es logica positiva) y todas las otras salidas estaran en 0. muchos decodificadores se diseñan para producir salidas activas con un 0(logica negativa donde la salida seleccionada es 0 mientras que las otras son 1). esto ultimo de indica

CODIFICADORES: un codificador tiene un numero de lineas de entrada, de las cuales solo na es activa(ya sea con logica positiva o negativa) en un tiempo dado y produce un codigo de salida de N bits, dependiendo de cual entrada esta activa. osea, el codificador hace el proceso contrario del decodificador.

SUMADORES

Antes de empezar quisiera recordarles las compuertas XOR (el símbolo de la operación es un signo de más circunscrito pero por comodidad usaremos aquí el ◊ para no tener que agregar una imagen cada vez que se requiera mostrar el signo. La XOR u OR exclusivo es parecida a la OR con la única diferencia que para cuando sus entradas son ambas 1 la salida es cero. La función XOR pude por supuesto ser presentado con compuertas AND, OR y NOT. Por ejemplo, la función F = A ◊ B , es también F = A'B+AB'. Existe también la compuerta XNOR o NOR exclusivo que es la función negada de la XOR. El símbolo de ésta es un punto en el centro de un círculo. La función F= A XNOR B tiene su equivalencia en F = AB+A'B'. Recuerden que los diagramas de las compuertas XOR y XNOR son:

y

respectivamente.

El circuito semisumador (o H.A. Por Half Adder) es aquel que realiza la suma de dos bits SIN tomar en cuenta algún posible acarreo previo.

Digamos que A y B son los bits a sumar, que S es la suma de ellos y que C_o es el bit de acarreo de salida, la tabla de la verdad de este circuito es:

A	B	S	Co
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Vemos entonces que C_o(A,B)=∑(3) y que S(A,B)=∑(1,2). Resolviendo estas funciones obtenemos que: C_o = AB y S = A'B + AB'. Si ven la última función se dará cuenta de por qué razón les hablé antes de la compuerta XOR. O sea, que S=A◊B. La diagramación de este circuito es:

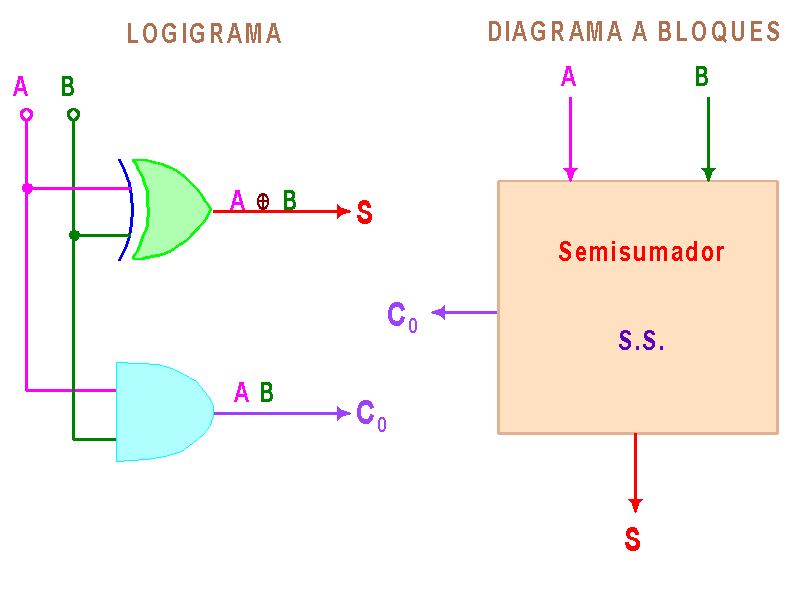
Pero este circuito nos serviría como sumador de un sólo bit (o para el bit menos significativo de una suma) pero en realidad es poco util para sumas de varios bits. En los casos que se requiera un sumador de varios bits, se hace uso de un Sumador Completo (F.A. Por Full Adder).

Veamos entonces como sería un sumador completo de 1 bit (lo que es el IC 7480 internamente).

Digamos que A y B son los bits a sumar, que S es la suma de ellos, que C_i es el acarreo de entrada y que C_o es el bit de acarreo de salida, la tabla de la verdad de este circuito es:

Ci	A	B	Co	S
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

De la tabla observamos que: C_o(C_i,A,B)=∑(3,5,6,7) y que S(C_i,A,B)=∑(1,2,4,7). O sea que C_o=A'BC_i+AB'C_i+ABC_i'+ABC_i y S=A'B'C_i+A'BC_i'+AB'C_i'+ABC_i. Simplificando vemos que:

C_o=AB+AC_i+ BC_i

y que S=C_i'(A'B+AB')+C_i(A'B'+AB), como (A'B'+AB)=(A'B+AB')'=(A◊B)' (XOR es una XNOR negada), si cambiamos las variables (para hacerlo mas fácil) y hacemos (A◊B)=T => S=C_i'T+C_iT'S = C_i◊T , entonces =>

S=C_i◊A◊B

Si doble negamos la función del acarreo de salida para implementar con compuertas NAND, obtendríamos la función C_o=[(AB)'(AC_i)'(BC_i)']' y el diagrama del circuito se vería:

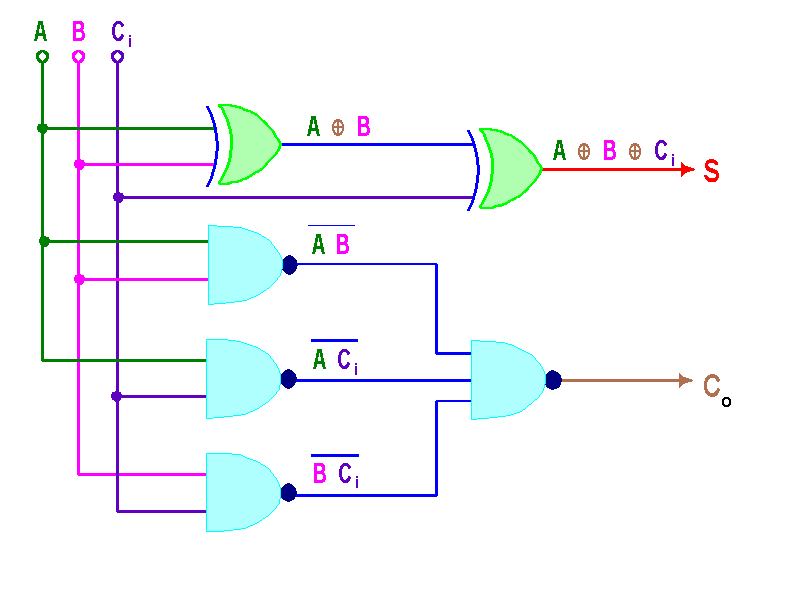
Este es un sumador completo de un bit, el mismo implementado en el IC 7480. En forma de bloque veríamos algo como:

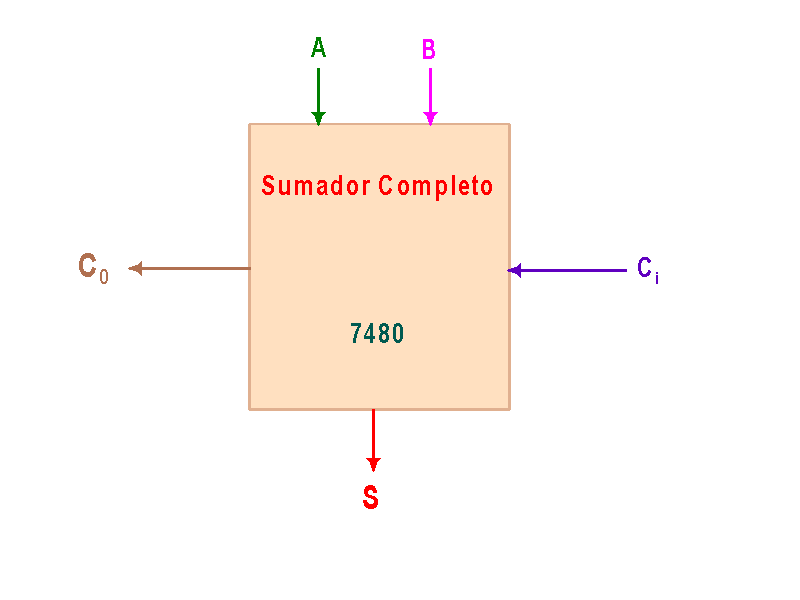
Estas implementaciones son realizadas con puras compuertas y los IC's usados usan menos de 10 de ellas por lo que estos sumadores son a nivel de SSI. Si queremos construir un sumador de, por ejemplo, 4 bits, deberemos poner en cascada cuatro sumadores completos de un bit tal como se muestra a continuación:

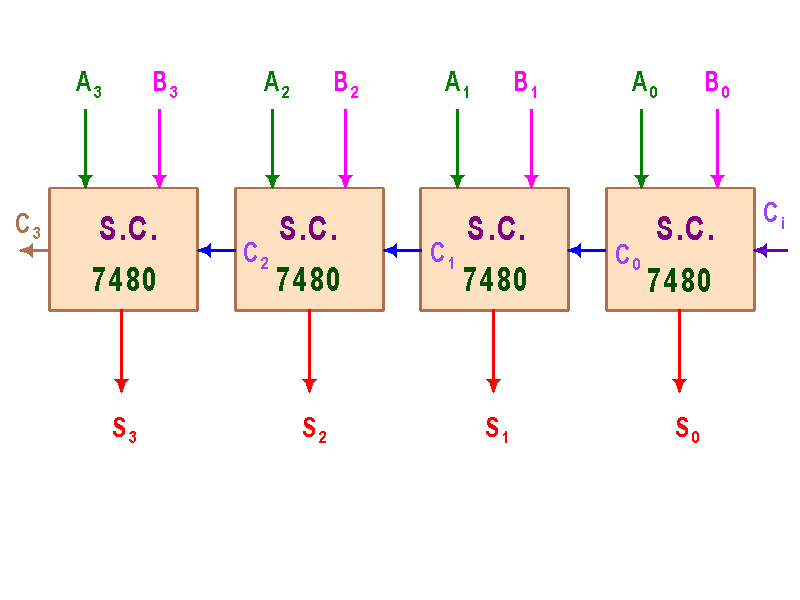
Esto no es más que el IC 7483 (que es un sumador a escala MSI debido al número de compuertas que éste usa).

El IC7483 es algo como:

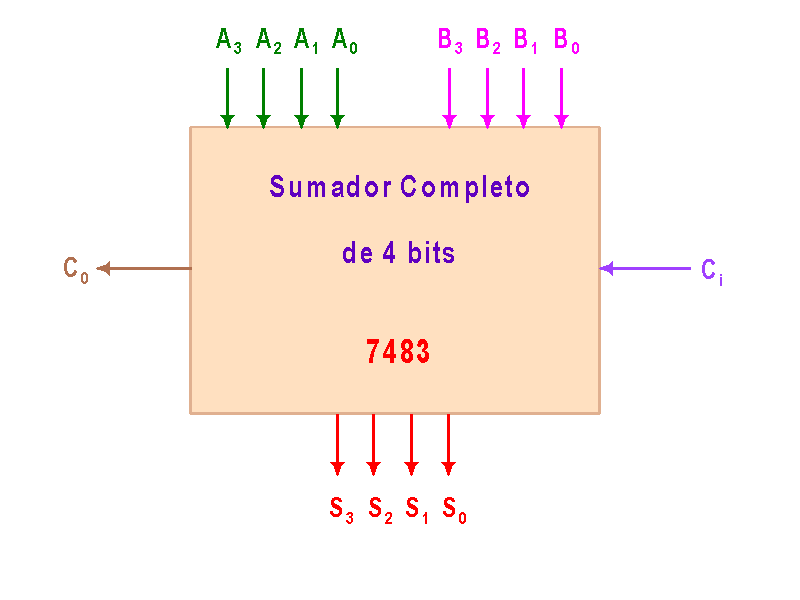
y estos sumadores a su vez también pueden ser organizados en cascada para implementar sumadores de 8, 12, 16, ... 4n, bits. El acarreo de entrada del primer sumador (quien incluirá el bit menos significativo) debe ir a tierra para indicar el cero.

Referencias
http://lasclases.com/CircuitosLogicos/tema8.html
Antonio Rodriguez, Isabel Vera