PRACTICA II. SIMPLIFICACION DE FUNCIONES

ESTE ES EL LINK PARA VISUALIZAR EL DOCUMENTO EN TAMAÑO ORIGINAL

https://docs.google.com/document/pub?id=10tp_YHkiTwClJmeaRX6f-JuG_qe9qMmcCShRb-Cg3yc

ESTE LINK ES PARA VISUALIZAR EL DOCUMENTO EN TAMAÑO COMPLETO

SSI y MSI

SSI y MSI son niveles de integración de compuertas lógicas.

Los niveles de integración son:

SSI: (Small-Scale Integration o integración a pequeña escala). Es el nivel de integración más básico y comprende todos aquellos circuitos integrados (desde ahora IC por sus siglas en inglés) que poseen hasta un máximo de diez (10) compuertas. En este nivel tenemos las compuertas lógicas como las NAND (por ejemplo, el IC 7400 tiene 4 compuertas NAND de dos entradas), las NOT (IC 7404 con 6 compuertas NOT), las AND (IC 7408 de 4x2), las OR (IC 7432 de 4x2), las XOR (IC 7486), memorias de 1 bit, flip-flops, el IC7480 que es un sumador completo de 1 bit, etc. Estas compuertas integran de 10 a 100 transistores.

MSI: (Medium-Scale Integration o integración de mediana escala). Es el nivel de integración que le sigue al SSI. Comprenden IC de que tienen entre 10 y 100 compuertas (entre 100 y 1000 transistores). En este campo tenemos memorias de palabra (8 bits), multiplexores, decodificadores, sumadores completos -entre ellos el IC7482 que es de 2 bits y el 7483 que es de 4 bits-, registros, contadores, etc.)

DECODIFICADORES: un decidificador es un cicuito combinacional que convierte la informacion binaria de n lineas de entradas a un maximo de 2^n lineas unicas de salida. para cada una de las combinaciones de entrada solo una de las salidas estara activada con un 1 (para cuando es logica positiva) y todas las otras salidas estaran en 0. muchos decodificadores se diseñan para producir salidas activas con un 0(logica negativa donde la salida seleccionada es 0 mientras que las otras son 1). esto ultimo de indica

CODIFICADORES: un codificador tiene un numero de lineas de entrada, de las cuales solo na es activa(ya sea con logica positiva o negativa) en un tiempo dado y produce un codigo de salida de N bits, dependiendo de cual entrada esta activa. osea, el codificador hace el proceso contrario del decodificador.

SUMADORES

Antes de empezar quisiera recordarles las compuertas XOR (el símbolo de la operación es un signo de más circunscrito pero por comodidad usaremos aquí el ◊ para no tener que agregar una imagen cada vez que se requiera mostrar el signo. La XOR u OR exclusivo es parecida a la OR con la única diferencia que para cuando sus entradas son ambas 1 la salida es cero. La función XOR pude por supuesto ser presentado con compuertas AND, OR y NOT. Por ejemplo, la función F = A ◊ B , es también F = A'B+AB'. Existe también la compuerta XNOR o NOR exclusivo que es la función negada de la XOR. El símbolo de ésta es un punto en el centro de un círculo. La función F= A XNOR B tiene su equivalencia en F = AB+A'B'. Recuerden que los diagramas de las compuertas XOR y XNOR son:

y

respectivamente.

El circuito semisumador (o H.A. Por Half Adder) es aquel que realiza la suma de dos bits SIN tomar en cuenta algún posible acarreo previo.

Digamos que A y B son los bits a sumar, que S es la suma de ellos y que C_o es el bit de acarreo de salida, la tabla de la verdad de este circuito es:

A	B	S	Co
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Vemos entonces que C_o(A,B)=∑(3) y que S(A,B)=∑(1,2). Resolviendo estas funciones obtenemos que: C_o = AB y S = A'B + AB'. Si ven la última función se dará cuenta de por qué razón les hablé antes de la compuerta XOR. O sea, que S=A◊B. La diagramación de este circuito es:

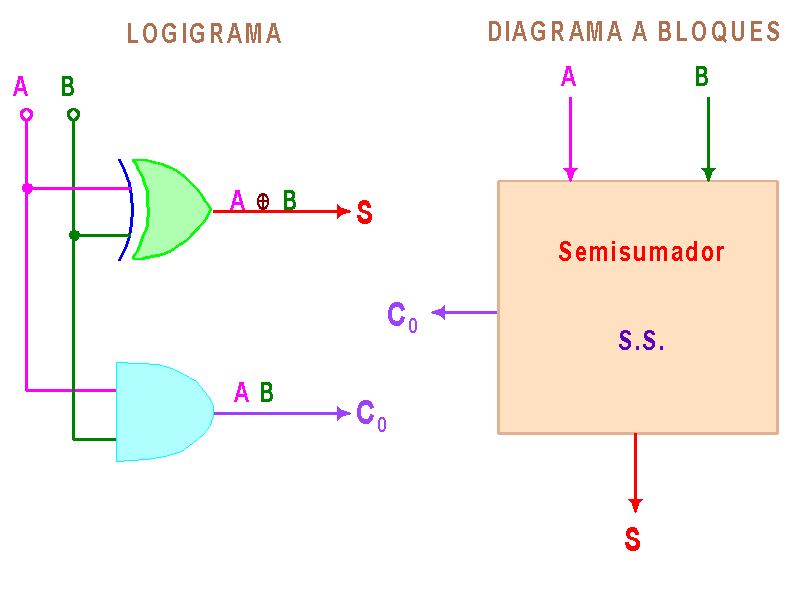
Pero este circuito nos serviría como sumador de un sólo bit (o para el bit menos significativo de una suma) pero en realidad es poco util para sumas de varios bits. En los casos que se requiera un sumador de varios bits, se hace uso de un Sumador Completo (F.A. Por Full Adder).

Veamos entonces como sería un sumador completo de 1 bit (lo que es el IC 7480 internamente).

Digamos que A y B son los bits a sumar, que S es la suma de ellos, que C_i es el acarreo de entrada y que C_o es el bit de acarreo de salida, la tabla de la verdad de este circuito es:

Ci	A	B	Co	S
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

De la tabla observamos que: C_o(C_i,A,B)=∑(3,5,6,7) y que S(C_i,A,B)=∑(1,2,4,7). O sea que C_o=A'BC_i+AB'C_i+ABC_i'+ABC_i y S=A'B'C_i+A'BC_i'+AB'C_i'+ABC_i. Simplificando vemos que:

C_o=AB+AC_i+ BC_i

y que S=C_i'(A'B+AB')+C_i(A'B'+AB), como (A'B'+AB)=(A'B+AB')'=(A◊B)' (XOR es una XNOR negada), si cambiamos las variables (para hacerlo mas fácil) y hacemos (A◊B)=T => S=C_i'T+C_iT'S = C_i◊T , entonces =>

S=C_i◊A◊B

Si doble negamos la función del acarreo de salida para implementar con compuertas NAND, obtendríamos la función C_o=[(AB)'(AC_i)'(BC_i)']' y el diagrama del circuito se vería:

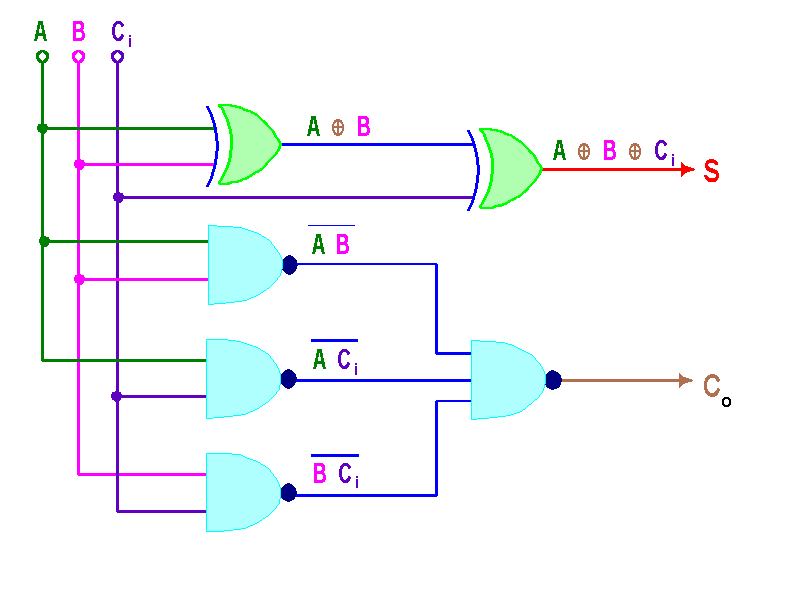
Este es un sumador completo de un bit, el mismo implementado en el IC 7480. En forma de bloque veríamos algo como:

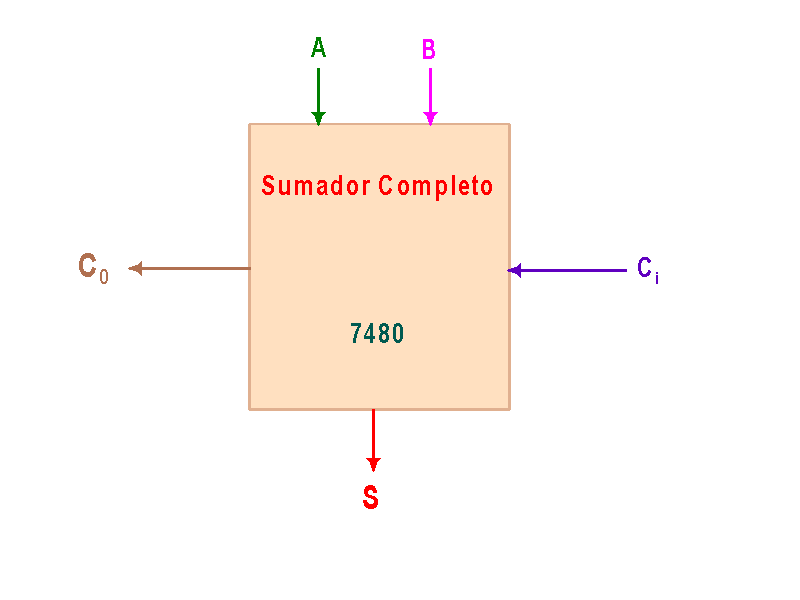
Estas implementaciones son realizadas con puras compuertas y los IC's usados usan menos de 10 de ellas por lo que estos sumadores son a nivel de SSI. Si queremos construir un sumador de, por ejemplo, 4 bits, deberemos poner en cascada cuatro sumadores completos de un bit tal como se muestra a continuación:

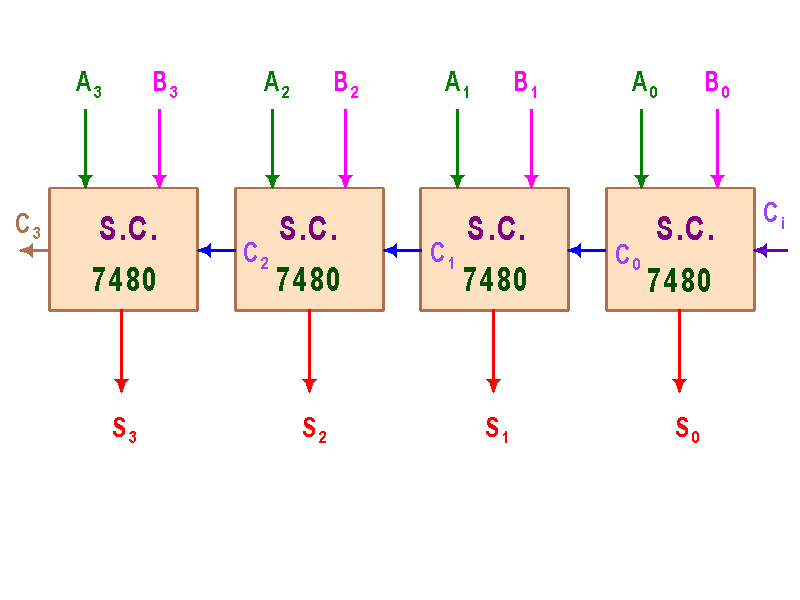
Esto no es más que el IC 7483 (que es un sumador a escala MSI debido al número de compuertas que éste usa).

El IC7483 es algo como:

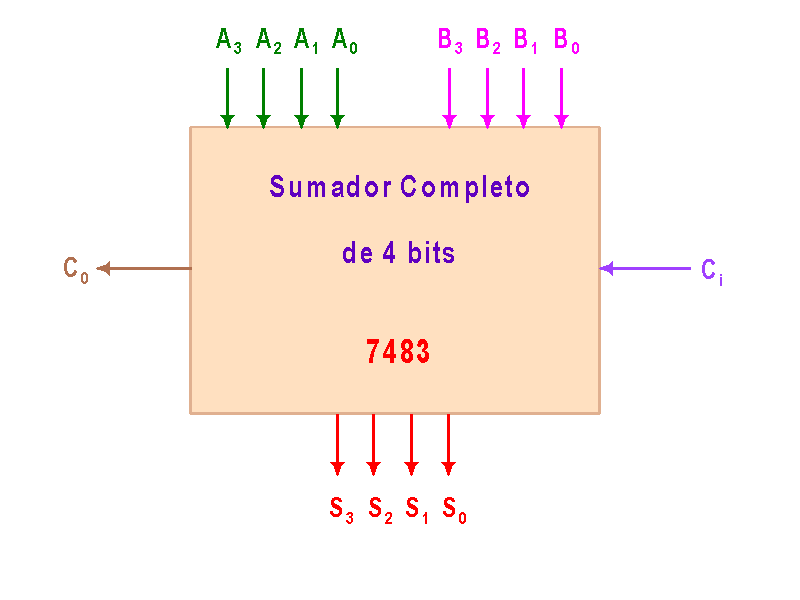
y estos sumadores a su vez también pueden ser organizados en cascada para implementar sumadores de 8, 12, 16, ... 4n, bits. El acarreo de entrada del primer sumador (quien incluirá el bit menos significativo) debe ir a tierra para indicar el cero.

Referencias
http://lasclases.com/CircuitosLogicos/tema8.html
Antonio Rodriguez, Isabel Vera

PRESENTACION DE FAMILIAS LOGICAS

- TTL

Las primeras puertas lógicas integradas eran mera copia directa de las puertas "o-negada" (Nor) con componentes discretos, mediante la conexión en paralelo de varios transistores bipolares NPN en emisor común; tales puertas dieron lugar a la primera familia lógica: RTL.

se mejoraron las características de estas puertas integradas, en cuanto a velocidad y a consumo, combinando una puerta "y" de diodos con un transistor inversor en emisor común; así se configuró la puerta "y-negada" (Nand) base de la familia DTL.
A partir de este esquema, se planteó una segunda mejora en velocidad y en consumo, añadiendo una etapa de salida amplificadora de intensidad (dos transistores en push-pull) y substituyendo los diodos por un transistor multi emisor.

La etapa de salida de dos transistores NPN ( totem pole: «palo de tótem») aumenta la intensidad suministrable y disminuye la resistencia de salida; el transistor multi emisor mejora considerablemente la conmutación de la puerta (en una primera aproximación, su comportamiento puede ser analizado en términos de diodos:

La clave del funcionamiento de la puerta TTL es el sentido en que circula la intensidad que la base del transistor multi emisor recibe desde la resistencia de 4K: - si dicha corriente va «hacia fuera», es decir, si alguna de las entradas está conectada a 0, el transistor T se encontrará en corte y el transistor T1, en colector común, transmite un 1 a la salida;
cuando todas las entradas se encuentran a 1 dicha intensidad circula «hacia dentro», hacia la base del transistor T, que se satura y lleva también a saturación al transistor T2, que pone la salida a 0. [Un 0 en una entrada supone una intensidad «hacia fuera», de forma que una entrada TTL «al aire» equivale a un 1, salvo efectos de ruido .]
Los tiempos de propagación de la serie TTL estándar son del orden de 10 ns. y el consumo promedio es de unos 2 mA (10 mW).

La serie 74LS (low power Schottky) mejora en gran medida a la serie estándar en cuanto a consumo (0,4 mA), manteniendo la velocidad de trabajo en valores análogos e incluso, algo superiores. La disminución del consumo se deriva del empleo de resistencias de mayor valor, lo cual acarrea un aumento de las constantes de tiempo asociadas; este efecto queda compensado por la inclusión de un diodo Schottky entre base y colector de los transistores que impide su saturación (desvía la corriente de base hacia el colector antes de entrar en una saturación profunda) y, con ello, aumenta su velocidad de conmutación.

La familia TTL proporcionó la base del gran desarrollo que tuvieron los sistemas digitales durante la década de los 70; su amplia difusión y utilización favoreció la aparición de diversas series derivadas de la mejora de características concretas, una de las cuales, la serie LS ha sustituido por completo a la serie estándar inicial y es la que se ha seguido utilizando a lo largo de la década de los 80.

la serie 74ALS (advanced LS) presenta tiempos por debajo de 4 ns, mientras que las series 74F (fast-TTL) y 74AS (advanced Schottky) ofrecen tiempos de propagación del orden de 2,5 ns y 1,5 ns, respectivamente, a costa de un mayor consumo (por utilizar resistencias de menor valor).
La serie 74LS sigue siendo útil para «recambio y mantenimiento» de los numerosos sistemas digitales que han sido construidos con ella (o con la serie estándar 74), la serie 74ALS se emplea en circuitos «interbús» (aplicación que consideraremos un poco más adelante) y la serie 74F resulta adecuada para diseños de muy alta velocidad de trabajo (frecuencias superiores a los 100 MHz).

CMOS

La tecnología CMOS (Complementary Metal-Oxide Semiconductor): lógica MOS complementaria, se basa basicamente del uso de dos transistores de efecto de campo a la salida del circuito, de canal n (NMOS) y de canal p (PMOS).

El proceso de fabricación de CMOS es más simple que el TTL y tiene una mayor densidad de integración, lo que permite que se tengan más circuitos en un área determinada de sustrato y reduce el costo por función. La gran ventaja de los CMOS es que utilizan solamente una fracción de la potencia que se necesita para la serie TTL de baja potencia (74L00), adaptándose de una forma ideal a aplicaciones que utilizan la potencia de una batería.

El inconveniente de la familia CMOS es que es más lenta que la familia TTL, aunque la nueva serie CMOS de alta velocidad “HCMOS” (SERIES HC y HCT), que vio la luz en 1983, puede competir con las series bipolares avanzadas en cuanto a elocidad y disponibilidad de corriente, y con un consumo menor, con las series 74 y 74LS.

Los primeros productos de familias lógicas CMOS se denominaron como circuitos integrados de serie 4000, 4001, etc. de los cuales esta connotación fue adoptada por todos los fabricantes.

Puertas lógicas de la familia CMOS

· INVERSORES CMOS

· COMPUERTA NAND CMOS

· COMPUERTA NOR CMOS

· COMPUERTAS AND Y OR

Inversor CMOS:

Un dispositivo CMOS consiste en distintos dispositivos MOS interconectados para formar funciones lógicas. Los circuitos CMOS combinan transistores PMOS y NMOS, cuyos símbolos más comunes son los que se muestran en la Figura

El circuito mostrado en la Figura 2 (a) representa un INVERSOR CMOS y está formado por un transistor de canal tipo P (QP1) y otro de canal tipo N (QN1).

La circuitería del INVERSOR CMOS básico se muestra en la Figura 2 (a). El INVERSOR CMOS tiene

dos MOSFET en serie de modo que, el dispositivo con canales P tiene su fuente conectada a + VDD (un voltaje positivo) y el dispositivo de canales N tiene su fuente conectada a masa. Las compuertas de los dos dispositivos se interconectan con una entrada común. Los drenajes de los dos dispositivos se interconectan con la salida común.

A continuación, consideremos el caso donde A1 = 0 V (la entrada A1 está en nivel bajo (‘0’)). QP1 tiene ahora su compuerta en un potencial negativo en relación con su fuente, en tanto que QN1 tiene VGS = 0 V.

De este modo, QP1 estará encendida con RON=1 k y QN1 apagada con ROFF = 10

10, produciendo un F de aproximadamente + VDD. En resumen QP1 se activa y el transistor QN1 se pone en estado de corte. El resultado es un camino de baja impedancia de VDD a la salida F y uno de alta impedancia de tierra a la salida.

Como se puede observar, los transistores operan de forma complementaria. Cuando la tensión de entrada se encuentra en alto (1 lógico), el transistor NMOS entra en estado de conducción y el transistor PMOS entra en corte, haciendo que la salida quede en bajo (0 lógico). La situación inversa ocurre cuando la tensión se encuentra en bajo.

Características de la serie CMOS

Series 4000/14000

Las primeras series CMOS fueron la serie 4000, que fue introducida por RCA y la serie14000 por Motorola. La serie original es la 4000A; la 4000B representa mejora con respecto a la primera y tiene mayor capacidad de corriente en sus salidas. A pesar de la aparición de la nueva serie CMOS, las series 4000 siguen teniendo uso muy difundido. La serie 4000A es la línea más usada de Circuitos Integrados digitales CMOS, contiene algunas funciones disponibles en la serie TTL 7400 y está en expansión constante. Algunas características más importantes de esta familia lógica son:

a) La disipación de potencia de estado estático de los circuitos lógicos CMOS es muy baja.
b) Los niveles lógicos de voltaje CMOS son 0 V para 0 lógico y VDD para 1 lógico. El suministro VDD
puede estar en el rango 3 V a 15 V para la serie 4000. La velocidad de conmutación de la familia CMOS 4000A varía con el voltaje de la fuente.(consultar el apartado de los niveles de voltaje).
c) Todas las entradas CMOS deben estar conectadas a algún nivel de voltaje.

Serie 74C

Esta serie CMOS su característica principal es que es compatible terminal por terminal y función por función, con los dispositivos TTL que tienen el mismo número (muchas de las funciones TTL, aunque no todas, también se encuentran en esta serie CMOS). Esto hace posible remplazar algunos circuitos TTL por un diseño equivalente CMOS. Por ejemplo, 74C74 contiene dos flip-flops tipo D disparados por flanco y tiene la misma configuración de terminales que el CI TTL 7474, que también ofrece dos flipflops tipo D disparados por flanco. El resto de las características son iguales a la serie 74C.

Las series HC/ HCT tienen como característica principal su alta velocidad.

Serie 74HC (CMOS de alta velocidad)

Esta es una versión mejor de la serie 74C. La principal mejora radica en un aumento de diez veces en la velocidad de conmutación (comparable con la de los dispositivos de la serie 74LS de TIL). Otra mejora es una mayor capacidad de corriente en las salidas. La serie 74HC son los CMOS de alta velocidad, tienen un aumento de 10 veces la velocidad de conmutación. La serie 74HCT es también de alta velocidad, y también es compatible en lo que respecta a los voltajes con los dispositivos TTL.

Serie 74HCT
Esta serie también es una serie CMOS de alta velocidad, y está diseñada para ser compatible en lo que respecta a los voltajes con los dispositivos TTL, es decir, las entradas pueden provenir de salidas TTL (esto no es cierto para las demás series CMOS).

Referencias:
http://www.mitecnologico.com/Main/FamiliasLogicasTtl

http://www.angelfire.com/la/SEMICONDUCTORES/TTL.html
Universidad del Táchira
Departamento de Ingeniería Electrónica
San Cristóbal, Estado Táchira, Venezuela

SIMBOLOGIA ESTANDAR DE LA NORMA IEEE/ANS 91-1984

Simbologia estandar

Las puertas logicas son circuitos electrónicos que implementan operaciones básicas de lógica binaria cuyo resultado puede ser verdadero o falso.
El paralelismo entre las operaciones binarias de la loica y las operaciones binarias de los sistemas digitales ha convertido a las puertas lógicas en los elementos básicos que componen los circuitos diitales.
Las líneas conectadas a la izquierda del símbolo de una puerta lógica son las entradas
A la derecha del símbolo de una puerta lógica hay una única línea conectada que representa la salida.

El estado de las entradas y salidas de una puerta lógica se representa de la siguiente manera
Falso:nivel lógico bajo o 0 binario
Verdadero: nivel lógico alto o 1 binario

TABLA DE VERDAD
El funcionamiento de una puerta lógica puede caracterizarse usando una tabla de verdad.
Una tabla de verdad muestra el valor de la salida para cada una de las posibles combinaciones de los valores de las entradas ,para simplificar la tabla es frecuente representar los niveles bajos con 0 y los niveles altos con 1, dada una puerta lógica de n entradas, el número de filas de la tabla de verdad será igual al numero de posibles combinaciones de las entradas
Las puertas lógicas digitales se clasifican en :

Puertas lógicas digitales
Puertas lógicas básicas
NOT
AND
OR
NAND
NOR
XOR
XNOR

LA PUERTA LOGICA NOT
La puerta logica NOT, tambien llamada inversor, realiza la operacion lógica conocida como inversión o complementación.
El inversor cambia de un nivel lógico al nivel opuesto
Si la entrada esta a nivel bajo, la salida estará a nivel alto.
Si la entrada esta a nivel alto, la salida estará a nivel bajo.

EL INDICADOR DE NEGACION

El indicador de negacion es un circulo que, cuando aparece ala entrada o salida de una puerta logica, indica complementacion o inversion.

Cuando se encuentra en una entrada quiere decir que se invierte el valor de la entrada.
Cuando se encuentra en una salida quiere decir que se invierte el valor de la salida.

EXPRESION LOGICA DE LA PUERTA NOT

Las magnitudes logicas pueden representarse con simbolos denominados variables. Una variable booleana se designa mediante un nombre generalmente una letra, los posibles valores de una variable booleana son 0 y 1.

El complemento o negacion de una variable se expresa mediante una barra encima de la letra.si una variable vale 1 su complemento vale 0 y viceversa.

LA PUERTA LOGICA AND

El proposito de una puerta logica AND es determinar cuando ciertas condiciones de entrada son verdaderas de forma simultanea.

• Se genera un nivel alto a la salida solo cuando todas las entradas estan en un nivel alto.
• Si cualquiera de las entradas esta a nivel bajo, se genera un nivel bajo a la salida independientemente del resto de las entradas.
  

EXPRESION LOGICA DE LA PUERTA AND
Una puerta logica AND realiza una operacion que se denomina multiplicacion logica. La multiplicacion logica se representa matematicamente colocando un punto entre dos variables o escribiendo las dos variables juntas, la multiplicacion logica sigue las reglas basicas de la multiplicacion binaria.

PUERTA LOGICA OR

El proposito de una puerta logica OR es determinar cuando una o mas de sus entradas esta en nivel alto.

se genera un nivel bajo a la salida solo cuando todas las entradas esta a un nivel bajo, sin embargo si cualquiera de las entradas esta a un nivel alto se genera un nivel alto a las salida independientemente al resto de las entradas.

EXPRESION LOGICA DE LA PUERTA OR

Una puerta logica OR realiza una operacion que se denomina suma logica. La suma logica se representa matematicamente colocando un signo + entre dos variables.la suma logica sigue las siguientes reglas basicas de la suma binaria, excepto en el caso de la suma de dos unos, ya que no existe el acarreo.

LA PUERTA LOICA NAND

La puerta logica NAND es muy popular porque es universal, es posible diseñar un circuito digital unicamente utilizando puertas NAND.

El termino NAND es una contraccion de NOT-AND e indica una puerta AND con la salida complementada.

Una puerta logica NAND funciona de una forma contraria a una puerta logica AND, se genera un nivel bajo a la salida solo cuando todas estan a nivel alto. Si cualquiera de las entradas esta anivel bajo, se generara un nivel alto a la salida independientemente del resto de entradas.

EXPRESION LOGICA DE LA PUERTA NAND

Una puerta logica NAND realiza una operacion que equivale a complementar el resultado de una multiplicacion logica, esta expresion logica indica que estas dos variables se multiplican y luego el resultado se complementa.

LA PUERTA LOGICA NOR

la puerta logica NOR tambien muy popular, es decir, es posible diseñar un circuito digital utilizando unicamente puertas NOR. El termino NOR es una contraccion de NOT-OR e indica una puerta OR con la salida complementada.

Una puerta logica NOR funciona exactamente contraria a una puerta logica OR

• Se genera un nivel alto a la salida solo cuando todas las entradas estan a un nivel bajo.
• si cualquiera de las entradas esta a nivel alto, se genera un nivel bajo a la salida independientemente del resto de entradas.

EXPRESION LOGICA DE LA PUERTA NOR

una puerta logica NOR realiza a una operacion que equivale a complementar el resultado de una suma logica.
Esta expresion logica indica que las dos variables se suman y luego el resultado se complementa.

CITA:

• Fundamentos de sistemas digitales 7ma edicion

3er capitulo

Thomas L. Floyd

Prentice Hall , 2000

• Introduccion a la logica binaria

Oliverio J. Santana Jaria

Sistemas digitales Ingenieria tecnica en informatica de sistemas2006

Tarea 2

DIFERENTES TIPOS DE CODIGOS
Conversión de binario a decimal

El sistema de numeración binario u un sistema de posición donde cada dígito binario (bit) tiene un valor basado en su posición relativa al LSB. Cualquier número binario puede convenirse a su equivalente decimal, simplemente sumando en el número binario las diversas posiciones que contenga un 1. Por ejemplo: 1 1 1 0 1 12 de binario a decimal 1 x 25 + 1 x 24 + 1 x 23 + 0 x 22 + 1 x 2 + 1 = 6910.

Conversión de decimal a binario

Existen dos maneras de convenir un número decimal entero a su representación equivalente en el sistema binario.
El primer método es inverso al proceso descrito anteriormente. El número decimal se expresa simplemente como una suma de potencias de 2 y luego los unos y los ceros se escriben en las posiciones adecuadas de los bits. Por ejemplo:
45 = 32 + 8 + 4 + l = 25 + 0 + 23 +2 2 + 0 + 20
entonces es igual a 1 0 1 1 0 12
Pasar a decimal el binario 101011102
1 0 1 0 1 1 1 0
Entonces el número se forma tomando los residuos pero en forma inversa, es decir el primer digito será el último residuo y así sucesivamente. El número quedaría como sigue:
1 0 0 0 0 0 1 02

Operaciones Binarias
En lo que sigue se adopta como convención la lógica positiva, lo que implica: verdadero = 1 = activo, ------, falso = 0 = inactivo Hay cinco operaciones binarias básicas: AND, OR, NOT, XOR y ADD. La resta, multiplicación y división se derivan de estas cinco anteriores. Cualquiera sea la longitud de la palabra o palabras objeto de la operación, siempre se hace de a un bit por vez de derecha a izquierda (tal como si fuera una suma o resta con números decimales). Esto permite una definición de cada operación que es independiente de la longitud del o de los operando(s). La operación NOT es la única que se realiza sobre un sólo operando (es unaria), y las otras cuatro sobre dos operandos.
La operación AND (Y) tiene resultado 1 si sus dos operandos son ambos 1 La operación OR (O) tiene resultado 1 si cualquiera de sus operandos es 1 La operación XOR tiene resultado 1 si los operandos son distintos (uno en 0 y el otro en 1) La operación NOT (NO) tiene resultado 1 si el operando es 0 y viceversa La operación ADD (SUMA) se define igual que con los números decimales

AND
OR
XOR
NOT
SUMA
0 * 0 = 0
0 + 0 = 0
0 X 0 = 0
NOT 1 = 0
0 + 0 = 0
0 * 1 = 0
0 + 1 = 1
0 X 1 = 1
NOT 0 = 1
0 + 1 = 1
1 * 0 = 0
1 + 0 = 1
1 X 0 = 1
---
1 + 0 = 1
1 * 1 = 1
1 + 1 = 1
1 X 1 = 0
---
1 + 1 = 10

División

Reglas de la división binaria: 0/0 no permitida, 1/0 no permitida,0/1=0, 1/1=1
Es lo que hacemos en la suma decimal 5+5=10 (nos llevamos “1″ para la operación del dígito siguiente). Este llevarse “1″ es vastamente usado entre los procesadores digitales y tiene un nombre especial: carry (lo verá abreviado como CY, C o CF-por carry flag), lo que en castellano se traduce como “acarreo” (que suena muy mal, asi que le seguiremos llamando carry). Estas operaciones también se llaman “booleanas” ya que se basan en el álgebra de Boole (invito al lector a rememorar cuando en la escuela secundaria se preguntaba, igual que yo, si el álgebra de Boole le serviría alguna vez para algo). En un ordenador el sistema de numeración es binario -en base 2, utilizando el 0 y el 1- hecho propiciado por ser precisamente dos los estados estables en los dispositivos digitales que componen una computadora. Para sumar números, tanto en base 2 como hexadecimal, se sigue el mismo proceso que en base 10:
Podemos observar que la suma se desa- 1010 1010b rrolla de la forma tradicional; es decir: + 0011 1100b sumamos normalmente, salvo en el caso de
1 + 1 = 102 , en cuyo caso tenemos un acarreo
1110 0110b
de 1 (lo que nos llevamos).

Complemento a 2

En general, se define como valor negativo de un número el que necesitamos sumarlo para obtener 00h, por ejemplo: FFh Como en un byte solo tenemos dos nibbles, es + 01h decir, dos dígitos hexadecimales, el resultado e 0 (observar cómo el 1 más significativo subrayado 100h es ignorado). Luego FFh=−1. Normalmente, el bit 7 se considera como de signo y, si está activo (a 1) el número es negativo. Por esta razón, el número 80h, cuyo complemento a dos es él mismo, se considera negativo (−128) y el número 00h, positivo. En general, para hallar el complemento a dos de un número cualquiera basta con calcular primero su complemento a uno, que consiste en cambiar los unos por ceros y los ceros por unos en su notación binaria; a continuación se le suma una unidad para calcular el complemento a dos. Con una calculadora, la operación es más sencilla: el complemento a dos de un número A de n bits es 2n-A. Otro factor a considerar es cuando se pasa de operar con un número de cierto tamaño (ej., 8 bits) a otro mayor (pongamos de 16 bits). Si el número es positivo, la parte que se añade por la izquierda son bits a 0. Sin embargo, si era negativo (bit más significativo activo) la parte que se añade por la izquierda son bits a 1. Este fenómeno, en cuya demostración matemática no entraremos, se puede resumir en que el bit más significativo se copia en todos los añadidos: es lo que se denomina la extensión del signo: los dos siguientes números son realmente el mismo número (el −310): 11012 (4 bits) y 111111012 (8 bits).

Sistema de numeracion octal

El sistema de numeración octal es muy importante en el trabajo que se realiza en una computadora digital. Este tiene una base de ocho, lo cual significa que tiene ocho posibles dígitos: 0, 1, 2, 3, 4, 5, 6 y 7. Así, cada dígito de un número octal puede tener cualquier valor del 0 al 7. Conversi6n de octal a decimal.- Por tanto, un número octal puede convenirse fácilmente a su equivalente decimal multiplicando cada dígito octal por su valor posicional. Por ejemplo:
2748 = 2 x 82 + 7 x 81 + 4 x 80
2848 = 2 x 64 + 7 x 8 + 4 x 1
2848 = 18810

Conversion de decimal a octal

Un entero decimal se puede convertir a octal con el mismo método dc división repetida que se usó en la conversión de decimal a binario, pero con un factor de división dc 8 en lugar de 2. Por ejemplo:
con residuo 4
con residuo 4
con residuo 2
Al final resulta que:
16410 = 2448

Conversion de octal a binario

La ventaja principal del sistema de numeración octal es la facilidad con que se puede realizar la conversión entre números binarios y octales. La conversión de octal a binario se lleva a cabo conviniendo cada dígito octal en su equivalente binario dc 3 bits. Por medio de estas conversiones, cualquier número octal se conviene a binario, convirtiéndolo dc manera individual. Por ejemplo, podemos convertir 516, a binario de la siguiente manera:
5 1 6
001 110 entonces:
5168 = 1010011102


Conversion de binario a octal
La conversión de enteros binarios a octales es simplemente la operación inversa del proceso anterior. Los bits del número binario se agrupan en conjuntos de tres comenzando por el LSB. Luego, cada grupo se convierte a su equivalente octal. Por ejemplo: 111 001 101 110 7 1 5 6 entonces: 1110011011102 = 71568

Sistema de numeracion hexadecimal

Conversión de hexadecimal a decimal.- Un número hexadecimal se puede convenir a su equivalente decimal utilizando el hecho de que cada posición de los dígitos hexadecimales tiene un valor que es una potencia de 16. El LSD tiene un valor de l60 = 1; el siguiente dígito en secuencia tiene un valor de 161 = 16; el siguiente tiene un valor de 162 = 256 y así sucesivamente. Por ejemplo:
81216 = 8 x 162 + 1 x 161 + 2 x 160
81216 = 2048 + 16 + 2
81216 = 206610

Conversion de decimal a hexadecimal
Recuerde que efectuamos la conversión de decimal a binario por medio de la división repetida entre 2 y de decimal a octal por medio de la división repetida entre 8. De igual manera, la conversión de decimal a hexadecimal se puede efectuar por medio de la división repetida entre 16. Por ejemplo:
con residuo 7
con residuo 010
con residuo 1
entonces:
42310 = 1A716

Cinversion de hexadecimal a binario

Al igual que el sistema de numeración octal, el sistema hexadecimal se usa principalmente como método ‘taquigráfico” en la representación de números binarios. Es una tarea relativamente simple la de convertir un número hexadecimal en binario. Cada dígito hexadecimal se convierte en su equivalente binario de 4 bits. Por ejemplo:
6 D 2 3
1101 0010 0011 entonces:
6D2316 = 1101101001000112

Conversion de binario a hexadecimal
Esta conversión es exactamente la operación inversa del proceso anterior. El número binario se agrupa en conjuntos de cuatro bits y cada grupo se convierte a su dígito hexadecimal equivalente. Cuando es necesario se añaden ceros para completar un grupo de cuatro bits.
11101001102 = 0011 1010 0110
3 A 6
11101001102 = 3A616

Referencia1
Editado por:
Eduardo Guzman
Carlos Castro Bojorquez
Miguel Palomares
Grupo 1A
ISC
http://www.mitecnologico.com/Main/BinarioOctalYHexadecimalADecimal



Conversion de binario a codigo gray

1. El MSB del numero binario será el mismo para el código Gray.
2. Sumar el MSB del numero binario al bit situado a su derecha inmediata y anotar el resultado del numero en código Gray que estamos formando.
3. Continuar sumando bits a los bits situados a la derecha y anotando las sumas; hasta llegar al LSB.
4. El número en código Gray tendrá el mismo número de bits que el número binario.


Ilustraremos mejor esta explicación con un ejemplo:

Ejemplo: convertir el numero binario 0010 a código Gray

Aquí finaliza la conversión dado que ya llegamos al LSB del numero binario.

Entonces el numero binario 0010 equivale al 0011 en código Gray

CONVERSIÓN DE CÓDIGO GRAY A BINARIO

1. El bit izquierdo de código Gray será el MSB del numero binario.
2. El bit obtenido es sumado al segundo bit de la izquierda del código Gray, y el resultado se anotara a la derecha del numero binario a formar.
3. Este resultado se le suma al bit situado a la derecha inmediata del ultimo bit que sumamos y el resultado será el otro bit del número binario (se ordena de izquierda a derecha).
4. Repetir el paso anterior hasta llegar al bit mas a la derecha del código Gray.
5. El número de bits del numero binario deberá coincidir con el número de bits del número en código Gray.

Ejemplo: convertir el número en código Gray 1001 a numero binario


Referencia 2
http://ladelec.com/teoria/electronica-digital/158-codigo-gray.html